Mr. Branson bought 5 children tickets and 4 adult tickets.
Explanation:
Let x be number of children tickets
Let y be the number of adult tickets.
So There are total of 9 tickets sold.
x+ y = 9 ------a
Cost of each child ticket = $ 6.50
Cost of an adult ticket = $ 9.25
6.5 x + 9.25 y = 69.5 ----b
Now we have to multiply equation a by -6.5 and add it eq. b as,
- 6.5 x-6.5 y = -58.5
6.5 x + 9.25 y = 69.5
x - term gets cancelled and we can write as,
9.25 y - 6.5 y = 69.5 - 58.5
2.75 y = 11
y =
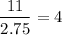
Plugin y = 4 in eq. a we will get x as,
x + y = 9
x+ 4 = 9
x = 9 - 4 = 5
So there are 5 children tickets and 4 adult tickets.