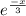Answer:
a) P(T>10 | T>7) = 0.3678
b) P(T>7+x | T>7) =
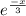
Explanation:
a)Conditional Probability that she needs to wait at least 3 more hours, given that she has already waited 7 hours

Three more hours means x = 7+3 = 10
P(T>10 | T>7) = P ( (T>10) ∩ (T>7)) / P (T>7)
P ( (T>10) ∩ (T>7)) = P (T>10)
P (T>10) = 1 - P (T≤10)
P (T≤10) =
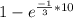
P (T≤10) = 0.9643
P (T>10) = 1 - P (T≤10) = 1 - 0.9643
P (T>10) = 0.03567
P (T>7) = 1 - P (T≤7)
P (T≤7) =
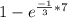
P (T≤7) = 0.903
P (T>7) = 1 - P (T≤7) = 1 - 0.903
P (T>7) = 0.097
P(T>10 | T>7) = 0.03567/0.097
P(T>10 | T>7) = 0.3678
b) The conditional probability that she needs to wait at least x more hours, given that she has already waited 7 hours
P(T>7+x | T>7) = P ( (T>7+x) ∩ (T>7)) / P (T>7)
P ( (T>7+x) ∩ (T>7)) = P (T>7+x)
P (T>7+x) = 1 - P (T≤7+x)
P (T≤7+x) =
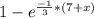
P (T>7+x) = 1 - P (T≤(7+x)) = 1 -
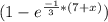
P (T>7+x) =
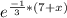
P (T>7+x) =

P (T>7+x) =
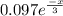
P (T>7) = 0.097
P(T>7+x | T>7) =
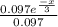
P(T>7+x | T>7) =