Answer:

Explanation:
The problem is
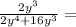
To solve this problem let us simplify the denominator by taking the greatest common factor of it
∵ The denominator is

∵ The factors of 2 are 1, 2
∵ The factors of 16 are 1, 2, 4, 8, 16
∴ The common factors of 2 and 16 are 1 and 2
∵ The greatest one is 2
∴ The greatest common factor of 2 and 16 is 2
The greatest common factor of a variable is the variable with the smallest exponent
∵ The smallest exponent of
 and y³ is 3
and y³ is 3
∴ The greatest common factor of
 and y³ is y³
and y³ is y³
∴ The greatest common factor of
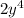 and 16y³ is 2y³
and 16y³ is 2y³
Divide each term of the denominator by the greatest common factor
∵
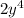 ÷ 2y³ = y
÷ 2y³ = y
∵ 16y³ ÷ 2y³ = 8
- The factorization of the denominator is 2y³(y + 8)
∴
 = 2y³(y + 8)
= 2y³(y + 8)
Substitute it in the fraction
∴
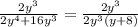
- Simplify the right hand side by dividing up and down by 2y³
∴
