Question

If a customer at a particular grocery store uses coupons, there is a 50% probability that the customer will pay with a debit card. Thirty percent of customers use coupons and 35% of customers pay with debit cards. Given that a customer pays with a debit card, the probability that the same customer uses coupons is ________.

Answer 1

The probability that a customer uses coupons given that the same customer pays with a debit card is P(C I D) = 0.428571 or about 0.43 (approximately 43%).

Explanation:

This is a question regarding the concept of conditional probability. The general formula for this is:

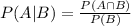`\\ P(A|B) = (P(A \cap B))/(P(B))` (1)

We can read the former as the probability of the event A given the event B is the probability that these two events occur simultaneously divided by the probability of event B.

We have to identify the events in the problem. We call the events as follows:

• Event D: pay with a debit card.
• Event C: pay with coupons.

Then, we have the next probabilities extracted from the question:

"If a customer at a particular grocery store uses coupons, there is a 50% probability that the customer will pay with a debit card" or

P(D|C) = 0.50

"Thirty percent of customers use coupons"

P(C) = 0.30

"...and 35% of customers pay with debit cards."

P(D) = 0.35

Then, the question is asking about P(C|D) = ?

Solving the question

Using formula (1) we can say that

`\\ P(C|D) = (P(C \cap D))/(P(D))`

`\\ P(D|C) = (P(D \cap C))/(P(C))`

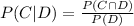
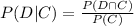
Thus

`\\ P(C|D)*P(D) = P(C \cap D)`

`\\ P(D|C)*P(C) = P(D \cap C)`

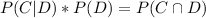
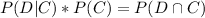
But

`\\ P(C \cap D) = P(D \cap C)`

Then

`\\ P(C|D)*P(D) = P(D|C)*P(C)`

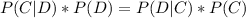
Solving the equation for P(C|D)

`\\ P(C|D) = (P(D|C)*P(C))/(P(D))`

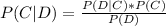
We already know the values for the right side of the equation and we can finally determine what the probability is. So

`\\ P(C|D) = (0.50*0.30)/(0.35)`

`\\ P(C|D) = (0.15)/(0.35)`

`\\ P(C|D) = (0.15)/(0.35) = 0.428571 \approx 0.43`

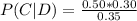
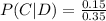
Thus, "given that a customer pays with a debit card, the probability that the same customer uses coupons is" 0.428571 (or about 0.43).

Answer 2

The probability that the same customer uses coupons given that a customer pays with a debit card is 0.43

Explanation:

The Р(A∩В) is obtained below:

Let A be the event that customer uses coupons and B be the event that customer pays with debit card.

From the information,

Р(A) = 0.30

P(B) = 0.35

and Р(B / A) = 0.50

P(A∩B) = P(A) P(B/A)

= 0.30x0.50

= 0.15

The probability that the same customer uses coupons given that a customer pays with a debit card is obtained below:

The required probability is,

P(AIB) = P(A∩B) / Р(В)

= (0.30x 0.50 ) / 0.35

= 0.15 / 0.35

= 0.43

The probability that the same customer uses coupons given that a customer pays with a debit card is 0.43