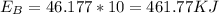Question

The explosion of a hydrogen bomb can be approximated by a fireball with a temperature of 7200 K, according to a report published in 1950 by the Atomic Energy Commission. (a) Calculate the total rate of radiant-energy emission for a 1.5 km diameter fireball that radiates as a blackbody. (b) Calculate the irradiation, G, on the wall of a house 40 km from the center of the blast. The blast occurs at an altitude of 16 km. (c) If the wall of the house is coated in red primer, estimate the total amount of radiation absorbed if the blast lasts 10 seconds. (d) If the wall is made of oak with a flammability limit of 650 K and a thickness of 1 cm, determine whether the wood catches on fire.

Answer 1

a

The rate of radiation of the energy is
`E_r = 1.523747635*10^9 W/m^2`

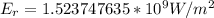
b

The irradiation is
`G =46.177\ kW/m^2`

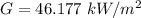
c

The amount of energy absorbed is
`E_B = 461.772 KJ`

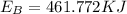
d

The oak Tree would catch fire because the temperature of the blast(7200 K) is higher than the flammability limit (650 K) of the oak tree and secondly the thickness is very small

Step-by-step explanation:

From the question we are told that

The temperature is
`T = 7200K`

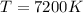
The diameter of the ball is
`d = 1.5 km = 1.5 *1000 = 1500m`

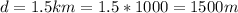
Hence the radius =
`= (1500)/(2) = 750m`

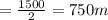
The total energy radiated can be mathematically represented as

`E = \sigma A T^4`

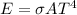
Where
`\sigma` is the Stefan-Boltzmann constant
`\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = 5.67*10^(-8) W \ \cdot m^(-2) K^(-4)`

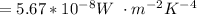
A is the area of a sphere =
`\pi d^2 = 3.142 * 1500^2 = 7.069500 *10 ^6\ m^2`

Substituting values we have

`E = 5,67*10^(-8) * 7.069500*10^6 * 7200^4`

`=1.077*10^(15) W`

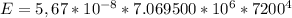
Now the state of the energy is mathematically represented as

`Rate \ of \ energy \ radiation (E_r)= (E)/(A) = \sigma T^4`

`= 5.67*10^(-8) * 7200^2`

`= 1.523747635*10^9 W/m^2`

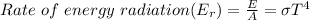
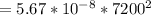
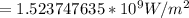
A sketch illustrating the b part of the question is shown on the first uploaded image

looking at the height at which the blast occurs(16km) as compared to the height of the wall we notice that the height of the wall is negligibly small

from the diagram x can be calculated as follows

`x = √(40^2 + 16^2)`

`= 43.0813 Km`

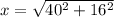
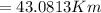
This value of x represents the radius of the blast(assuming it is spherical ) when it is at that wall

Now the irradiation G is mathematically represented as

`G = (E)/(4 \pi r^2)`

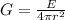
Here r = 43.0813 Km = 43.0813 × 1000 = 43081.3 m

`G= (1.077*10^15)/(4 \pi (431081.3^2))`

`G =46.177\ kW/m^2`

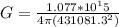
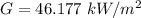
Generally the amount of energy absorbed can be mathematically represented as

`Amount \ of \ energy \ absorbed \ (E_B ) = G * t`

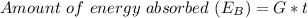
Where t is the time taken

Therefore
`E_B = 46.177 *10 = 461.77 KJ`