Question

Suppose our experimenter repeats his experiment on a planet more massive than Earth, where the acceleration due to gravity is g = 30 m/s². When he releases the ball from chin height without giving it a push, how will the ball's behavior differ from its behavior on Earth? Ignore friction and air resistance.

(Select all that apply.)
a. It will take more time to return to the point from which it was released.
b. It will smash his face.
c. Its mass will be greater.
d. It will take less time to return to the point from which it was released.
e. It will stop well short of his face.

Answer 1

Answer: a) It will take more time to return to the point from which it was released

Explanation: To determine how long it takes for the ball to return to the point of release and considering it is a free fall system, we can use the given formula:

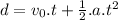`d=v_(0).t + (1)/(2) .a.t^(2)`, where:

d is the distance the ball go through;

v₀ is the initial velocity, which is this case is 0 because he releases the ball;

a is acceleration due to gravity;

t is the time necessary for the fall;

Suppose h is the height from where the ball was dropped.

On Earth:

h=0.t +
`(1)/(2).10.t^(2)`

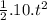
h = 5t²

`t_(T)` =
`\sqrt{(h)/(5) }`

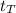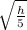
On the other planet:

h = 0.t +
`(1)/(2).30.t^(2)`

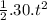
h = 15.t²

`t_(P)` =
`\sqrt{(h)/(15) }`

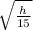
Comparing the 2 planets:

`(t_(T) )/(t_(P) ) = \frac{\sqrt{(h)/(5) } }\sqrt{{(h)/(15) } }`

`(t_(T) )/(t_(P) )` =
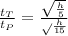
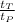`√(3)` or
`t_(T) = √(3).t_(P)`

Comparing the two planets, on the massive planet, it will take more time to fall the height than on Earth. In consequence, it will take more time to return to the initial point, when it was released.