Answer:
The steady state proportion for the U (uninvolved) fraction is 0.4.
Explanation:
This can be modeled as a Markov chain, with two states:
U: uninvolved
M: matched
The transitions probability matrix is:
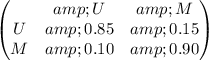
The steady state is that satisfies this product of matrixs:
![[\pi] \cdot [P]=[\pi]](https://img.qammunity.org/2021/formulas/mathematics/college/ogx13zfei5tlecbilr4yn9gce8a92rlw55.png)
being π the matrix of steady-state proportions and P the transition matrix.
If we multiply, we have:
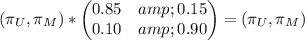
Now we have to solve this equations
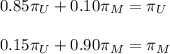
We choose one of the equations and solve:

Then, the steady state proportion for the U (uninvolved) fraction is 0.4.