Question

In a simple electric circuit, Ohm's law states that V=IRV=IR, where V is the voltage in volts, I is the current in amperes, and R is the resistance in ohms. Assume that, as the battery wears out, the voltage decreases at 0.01 volts per second and, as the resistor heats up, the resistance is increasing at 0.04 ohms per second. When the resistance is 300 ohms and the current is 0.01 amperes, at what rate is the current changing?

Answer 1

To solve this problem, apply the concepts given from Ohm's Law. From there we will obtain the derivative of the function with respect to time and with the previously given values we will proceed to find the change in current as a function of the derivative

`V = IR`

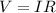
Here

I = Current

V = Voltage

R = Resistance

Taking the derivative we will have,

`(dV)/(dt) = (dI)/(dt)R + I (dR)/(dt)`

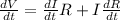
Our values are given as,

`(dV)/(dt) = -0.01`

`(dR)/(dt) = 0.04\Omega/s`

`R = 300\Omega`

`I = 0.01A`

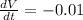
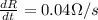
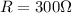
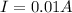
Replacing we will have that

`(dV)/(dt) = (dI)/(dt)R + I (dR)/(dt)`

`-0.01 = (dI)/(dt)(300\Omega) + (0.01A)(0.04\Omega/s)`

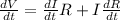
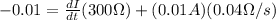
Rearranging to find the current through the time,

`(dI)/(dt) = (-0.01- (0.01A)(0.04\Omega/s))/((400\Omega))`

`(dI)/(dt) = -0.000026A/s`

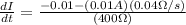
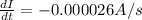
Therefore the change of the current is -0.000026A per second