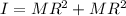Question

The moment of inertia of a thin ring of mass M and radius R about its symmetry axis is I C M = M R 2 . Kira is working the ring‑toss booth at a local carnival. While waiting for customers, Kira occupies her time by twirling one of the plastic rings of mass M and radius R about her finger. Model the motion of the plastic ring as a thin ring rotating about a point on its circumference. What is the moment of inertia of the plastic ring?

Answer 1

So total moment of inertia of the ring about its end is given as

`2MR^2`

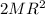
Step-by-step explanation:

As we know that the moment of inertia of the ring about its axis passing through COM is given by the formula

`I_(cm) = MR^2`

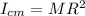
now we know that

if we wish to find the moment of inertia passing through an axis from its circumference which is parallel to the axis passing from COM is given by parallel axis theorem

So we will have

`I = I_(cm) + md^2`

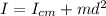
so here we have

`I = MR^2 + MR^2`

`I = 2MR^2`