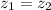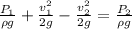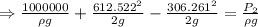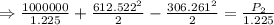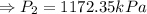Question

A converging-diverging nozzle with an exit to throat area ratio of 4.0 is designed to expand air isentropically to atmospheric pressure. Determine the exit Mach number at design conditions and the required inlet stagnation pressure. Also, calculate the back pressures corresponding to the various flow regimes for the nozzle.

Answer 1

0.9, 1172.35kPa

Step-by-step explanation:

Question (in proper order) Attached below

Air is flowing inside the throat has following inlet conditions

`P_(0)=1000 kPa`

`T_(0)=500 K`

`M=1.8`

`M=(u)/(c)=1.8`

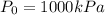
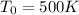
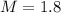
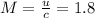
'u' is the speed of sound in the air

`\Rightarrow u=1.8* c`

`=1.8* 340.29`

`=612.522(m)/(sec)`

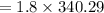
Therefore volumetric flow rate entering,

`Q=612.522* 0.0008`

`=0.4900176(m^(3))/(sec)`

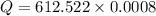
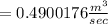
Using ideal gas equation

PV=nRT

`n=(PV)/(RT)`

`=(1000* 0.4900176)/(8.314* 500)`

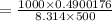
=0.117878 gmoles/sec

Therefore , mass flow rate

`Mass = 0.117878* 29`

`=3.4184 grams/sec`

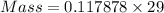
Given

`(A)/(A_(0))=2`

`\Rightarrow A=0.0016.m^(2)`

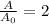
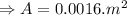
Using continuity equation

`A_(1)V_(1)=A_(2)V_(2)`

`\Rightarrow V_(2)=(A_(1)V_(1))/(A_(2))`

`=(0.0008* 612.522)/(0.0016)`

`=306.261(m)/(sec)`

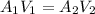
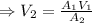
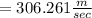
Hence exit velocity = 306.261 m/sec

Exit Mach number

`M=(u)/(c)=(306.261)/(340.29)=0.9`

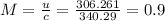
Temperature will remain same as 500 K

Now

Using Bernoulli's equation

`(P_(1))/(\rho g)+(v_(1)^(2))/(2g)+z_(1)=(P_(2))/(\rho g)+(v_(2)^(2))/(2g)+z_(2)`

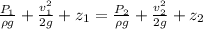
Here

`z_(1) = z_(2)`

`(P_(1))/(\rho g)+(v_(1)^(2))/(2g)-(v_(2)^(2))/(2g)=(P_(2))/(\rho g)`

`\Rightarrow (1000000)/(\rho g)+(612.522^(2))/(2g)-(306.261^(2))/(2g)=(P_(2))/(\rho g)`

`\Rightarrow (1000000)/(1.225)+(612.522^(2))/(2)-(306.261^(2))/(2)=(P_(2))/(1.225)`

`\Rightarrow P_(2)=1172.35kPa`