Question

A cylinder of mass 14.0 kg rolls without slipping on a horizontal surface. At a certain instant its center of mass has a speed of 9.0 m/s. (a) Determine the translational kinetic energy of its center of mass. J (b) Determine the rotational kinetic energy about its center of mass. J (c) Determine its total energy.

Answer 1

a) 567J

b) 283.5J

c) 850.5J

Step-by-step explanation:

given

Mass of the cylinder, m = 14kg

Speed of mass, v = 9m/s

To determine the Translational Kinetic Energy, we use KE = 1/2mv²

KE(trans) = 1/2 * 14 * 9²

KE(trans) = 567J

To determine the Rotational Kinetic Energy, we use = 1/2Iw²

KE(rot) = 1/2Iw² = 1/2 * 1/2mr² * (v/r) ²

KE(rot) = 1/4 * mv²

KE(rot) = 1/4 * 14 * 9²

KE(rot) = 283.5J

To determine the Total Energy, we sum up both the transnational and rotational energies = KE(trans) + KE(rot)

Total energy = 567J + 283.5J

Total energy = 850.5J

Answer 2

a) 567J

b) 283.5J

c)850.5J

Step-by-step explanation:

The expression for the translational kinetic energy is,

`E_r = (1)/(2) mv^2`

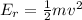
Substitute,

14kg for m

9m/s for v

`E_r = (1)/(2) (14) (9)^2\\= 567J`

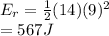
The translational kinetic energy of the center of mass is 567J

(B)

The expression for the rotational kinetic energy is,

`E_R = (1)/(2) Iw^2`

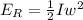
The expression for the moment of inertia of the cylinder is,

`I = (1)/(2) mr^2`

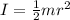
The expression for angular velocity is,

`w = (v)/(r)`

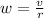
substitute

1/2mr² for I

and vr for w

in equation for rotational kinetic energy as follows:

`E_R = ((1)/(2)) ((1)/(2) mr^2)((v)/(r) )^2`

`= (mv^2)/(4)`

`E_R = (14 * 9^2 )/(4) \\\\= 283.5J`

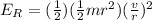
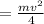
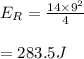
The rotational kinetic energy of the center of mass is 283.5J

(c)

The expression for the total energy is,

`E = E_r + E_R\\\\`

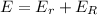
substitute 567J for E(r) and 283.5J for E(R)

`E = 567J + 283.5\\= 850.5J`

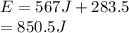
The total energy of the cylinder is 850.5J