Answer:
a) 567J
b) 283.5J
c)850.5J
Step-by-step explanation:
The expression for the translational kinetic energy is,
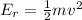
Substitute,
14kg for m
9m/s for v
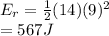
The translational kinetic energy of the center of mass is 567J
(B)
The expression for the rotational kinetic energy is,
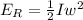
The expression for the moment of inertia of the cylinder is,
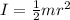
The expression for angular velocity is,
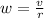
substitute
1/2mr² for I
and vr for w
in equation for rotational kinetic energy as follows:
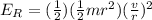
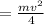
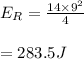
The rotational kinetic energy of the center of mass is 283.5J
(c)
The expression for the total energy is,
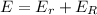
substitute 567J for E(r) and 283.5J for E(R)

The total energy of the cylinder is 850.5J