Answer:
Step-by-step explanation:
mass of bullet, mb = 11.5 g
velocity of bullet, vb = 265 m/s
Spring constant, K = 205 N/m
compression in spring, Δd = 35 cm = 0.35 m
Let m be the mass of wooden block.
Let v is the velocity of wooden block.
Use conservation of momentum
mb x vb = ( m + mb) x v
0.0115 x 265 = ( m + 0.0115) x v
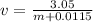 ... (1)
... (1)
Use conservation of energy
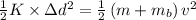
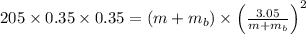
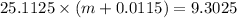
m = 0.36 kg