Answer:
Probability that the mean of their age is between 90 and 99 months is 0.97722 or 0.98.
Step-by-step explanation:
We are given that the average age of a vehicle registered in the United States is 8 years, or 96 months. Assume the standard deviation is 9 months.
Also, a random sample of 36 card is selected.
Firstly, Let
 = mean age of selected cars
= mean age of selected cars
The z score probability distribution for is given by;
Z =
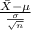 ~ N(0,1)
~ N(0,1)
where,
 = average age of a vehicle = 96 months
= average age of a vehicle = 96 months
 = standard deviation = 9 months
= standard deviation = 9 months
n = sample of cars = 36
Probability that the mean of their age is between 90 and 99 months is given by = P(90 <
 < 99) = P(
< 99) = P(
 < 99) - P(
< 99) - P(

 90)
90)
P(
 < 99) = P(
< 99) = P(
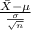 <
<
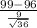 ) = P(Z < 2) = 0.97725
) = P(Z < 2) = 0.97725
P(

 90) = P(
90) = P(
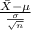

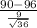 ) = P(Z
) = P(Z
 -4) = 1 - P(Z < 4)
-4) = 1 - P(Z < 4)
= 1 - 0.99997 = 0.00003
Therefore, P(90 <
 < 99) = 0.97725 - 0.00003 = 0.97722 ≈ 0.98
< 99) = 0.97725 - 0.00003 = 0.97722 ≈ 0.98
Hence, probability that the mean of their age is between 90 and 99 months is 0.98.