Question

A 0.560 kg snowball is fired from a cliff 14.2 m high with an initial velocity of 13.3 m/s, directed 26.0° above the horizontal. (a) Using energy techniques, find the speed of the snowball as it reaches the ground below the cliff. What is that speed (b) if the launch angle is changed to 26.0° below the horizontal and (c) if the mass is changed to 1.30 kg?

Answer 1

a) v = 21.34 m/s

b) v = 21.34 m/s

c) v = 21.34 m/s

Step-by-step explanation:

Mass of the snowball, m = 0.560 kg

Height of the cliff, h = 14.2 m

Initial velocity of the ball, u = 13.3 m/s

θ = 26°

The speed of the slow ball as it reaches the ground, v = ?

The initial Kinetic energy of the snow ball,
`KE_(0) = 0.5 mu^(2)`

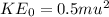
Potential energy of the snow ball at the given height, PE = mgh

Final Kinetic energy of the ball as it reaches the ground,
`KE_(f) = 0.5mv^(2)`

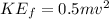
a) Using the principle of energy conservation,

`KE_(0) + PE = KE_(f) \\0.5mu^(2) + mgh = 0.5mv^(2)\\v^(2) =2( 0.5u^(2) + gh)\\v^(2) =u^(2) + 2gh\\v = \sqrt{u^(2) + 2gh} \\v = \sqrt{13.3^(2) + 2*9.8*14.2}\\v = 21.34 m/s`

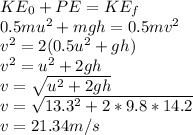
b) The speed remains v = 21.34 m/s since it is not a function of the angle of launch

c)The principle of energy conservation used cancels out the mass of the object, therefore the speed is not dependent on mass

v = 21. 34 m/s