Answer:
= 94.99%
Explanation:
From the given information ,
it is obvious that the black out schedule has each region without power on average μ = 2.5 hours per day.
The standard deviation of blackout times in this city is б = 0.31 hours
A local hospital in the area purchases a generator that will provide power to nonessential systems for 3.5 hours
The percentage of time will the hospital find themselves without power to these nonessential systems is as follows:
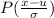
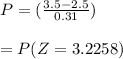
![[NORMSDIST(3.2258)]\\\\= 0.9994\\\\= 94.99%](https://img.qammunity.org/2021/formulas/mathematics/college/hnrs7d1m5upbx50dmgmip6ma5ian7v7lsg.png)
= 94.99%