Answer:
7.63 ksi
Step-by-step explanation:
Given that:
pitch(p) = 6 teeth/in
pressure angle
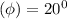
Pinion speed
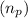 = 1200 rev/min
= 1200 rev/min
Power(H) = 15 hp
Teeth on gear
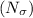 = 60
= 60
Teeth on pinion
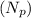 = 22
= 22
Face width (b) = 2 in
To find the diameter from the parameters above ; we have:
(d) =
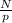
=
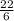
= 3.667 in
Using values of the Lewis factor Y for
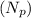 = 22
= 22
Y = 0.331
Then finding the velocity; we have the formula;
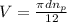
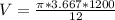
V = 1152 ft/min
For the cut or mi;;ed profile; the velocity factor can be determined as
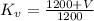
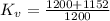

Then we proceed to determine the value of our tangential load also as follows:
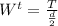

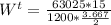
= 429.79 lbf
Finally ; the bending stress is calculated as :
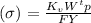
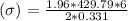
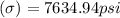
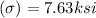
Thus, the bending stress is 7.63 ksi