
Let's solve ~
If it passes through x, then let's find x when y = 0
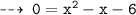
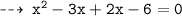


So, required values of x are 3 and -2
Now, let's differentiate the equation to get slope slope for tangent ~

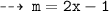
Now, plug in the values of x to find slopes of tangents
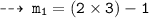
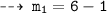
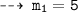
and
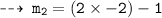
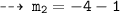
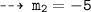
We know, tangent are normal are perpendicular. so let's find out slopes of normals m1' and m2'
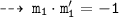


and
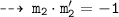

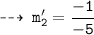

Now, write the equations of normals using point slope form :
Normal 1 : passing through (3 , 0), and slope = -1/5

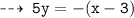
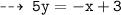
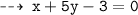
and
Normal 2 : passing through (-2 , 0), and slope = 1/5

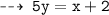
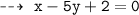
That's all for Aunty ~ hope it helps !