Question

Find The Eqn Of Normal To The Curve y= x² - x - 6 at The Point Where It Process x - axis.​

Answer 1

`\qquad\qquad\huge\underline{{\sf Answer}}♨`

Let's solve ~

If it passes through x, then let's find x when y = 0

`\qquad \tt \dashrightarrow \:0 = {x}^(2) - x - 6`

`\qquad \tt \dashrightarrow \: {x}^(2) - 3x + 2x - 6 = 0`

`\qquad \tt \dashrightarrow \:x(x - 3) + 2(x - 3) = 0`

`\qquad \tt \dashrightarrow \:(x - 3) (x + 2) = 0`

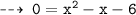
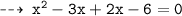
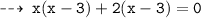
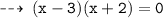
So, required values of x are 3 and -2

Now, let's differentiate the equation to get slope slope for tangent ~

`\qquad \tt \dashrightarrow \: m = (d)/(dx) ( {x}^(2) - x - 6)`

`\qquad \tt \dashrightarrow \: m = 2 x - 1`

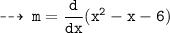
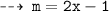
Now, plug in the values of x to find slopes of tangents

`\qquad \tt \dashrightarrow \: m _1 = (2 * 3) - 1`

`\qquad \tt \dashrightarrow \: m_1 = 6 - 1`

`\qquad \tt \dashrightarrow \: m _1 = 5`

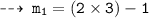
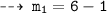
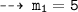
and

`\qquad \tt \dashrightarrow \:m_2 = (2 * - 2) - 1`

`\qquad \tt \dashrightarrow \:m_2 = - 4- 1`

`\qquad \tt \dashrightarrow \:m_2 = - 5`

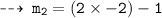
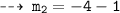
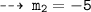
We know, tangent are normal are perpendicular. so let's find out slopes of normals m1' and m2'

`\qquad \tt \dashrightarrow \:m _1\cdot m_1 ' = - 1`

`\qquad \tt \dashrightarrow \:m _1' = (- 1)/(m_1)`

`\qquad \tt \dashrightarrow \:m _1' = (- 1)/( 5)`

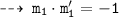
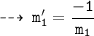
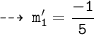
and

`\qquad \tt \dashrightarrow \:m _2\cdot m_2 ' = - 1`

`\qquad \tt \dashrightarrow \:m _2' = (- 1)/(m_2)`

`\qquad \tt \dashrightarrow \:m _2' = (- 1)/( -5)`

`\qquad \tt \dashrightarrow \:m _2' = (1)/( 5)`

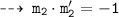
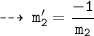
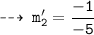
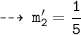
Now, write the equations of normals using point slope form :

Normal 1 : passing through (3 , 0), and slope = -1/5

`\qquad \tt \dashrightarrow \:y - 0 = - (1)/(5) (x - 3)`

`\qquad \tt \dashrightarrow \:5y = - (x - 3)`

`\qquad \tt \dashrightarrow \:5y = - x + 3`

`\qquad \tt \dashrightarrow \:x + 5y - 3 = 0`

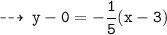
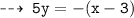
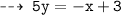
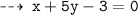
and

Normal 2 : passing through (-2 , 0), and slope = 1/5

`\qquad \tt \dashrightarrow \:y - 0 = (1)/(5) (x - ( - 2))`

`\qquad \tt \dashrightarrow \:5y = x + 2`

`\qquad \tt \dashrightarrow \ x - 5y + 2 = 0`

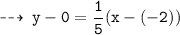
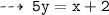
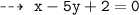
That's all for Aunty ~ hope it helps !