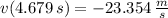Answer:
a)
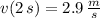 , b)
, b)
 , c)
, c)
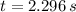 , d)
, d)
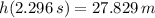 , e)
, e)
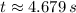 , f)
, f)
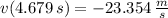
Explanation:
The velocity function can be derived by the differentiating the height function:
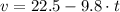
Velocities after 2 and 4 seconds are, respectively:
a)
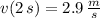
b)

The maximum height is reached when velocity is zero. Then:

c)
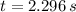
The maximum height is:
d)
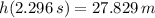
The time required to hit the ground is:
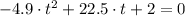
Roots of the second-order polynomial are:

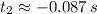
Only the first root is physically reasonable.
e)
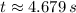
The velocity when the projectile hits the ground is:
f)