1 Answer

Raffaele · Answer 1 · 2021-08-11T04:45:05+0000

The measure of angle A is 42°

Step-by-step explanation:

Given that ABCD is a quadrilateral.

The measures of angles are
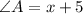$\angle A=x+5$ ,
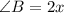$\angle B= 2x$ and
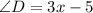
$\angle D=3x-5$

We need to determine the measure of angle A

The value of x:

Since, we know that the opposite angles of a quadrilateral add up to 180°

Thus, we have,

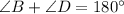
$\angle B+\angle D=180^(\circ)$

Substituting the values, we get,

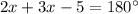
$2x+3x-5=180^(\circ)$

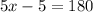
5x-5=180

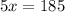
5x=185

x=37

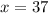
Thus, the value of x is 37

Measure of
$\angle A$ :

The measure of angle A can be determined by substituting
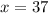x=37 in
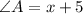$\angle A=x+5$ , we get,

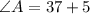
$\angle A=37+5$

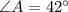
$\angle A=42^(\circ)$

Thus, the measure of angle A is 42°

Please log in or register to add a comment.