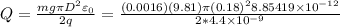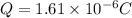Question

A parallel-plate capacitor is constructed of two horizontal 18.0-cm-diameter circular plates. A 1.6 g plastic bead with a charge of -4.4 nC is suspended between the two plates by the force of the electric field between them. What is the charge on the positive plate?

Answer 1

q2 = 3.96×10-⁴ × r²

Step-by-step explanation:

Let F = the force experienced by the bead in the electric field of the capacitor. This electric force just balances the weight of the bead. So the electric force = weight of the bead.

F = kq1×q2/r² = mg

m = 1.6g = 0.0016kg

g = 9.8m/s²

k1 = the electric force constant = 9.0×10⁹Nm²/C²

q1 = -4.4nC = -4.4×10-⁹ C

q2 = ?

r = distance between the plates

Re arranging the equation

q2 = mgr²/(k×q1)

q2 = 0.0016×9.8r²/(9.0×10⁹×4.4×10-⁹)

q2 = 3.96×10-⁴ × r²

Answer 2

The charge is
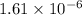`1.61*10^(-6)`Columbus.

Step-by-step explanation:

The electric field between two parallel plates it is:

`E=(\sigma)/(2\varepsilon_(0))` (1)

with σ the surface charge density of one plate and εo the permittivity of vacuum that is
`8.85419*10^(-12)(C^(2))/(Nm^(2))`. Surface charge density is the ratio between net charge (Q) and the surface (in our case the area (A) of the plate):

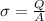`\sigma =(Q)/(A)` (2)

the area of a circle with diameter D is
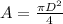`A=(\pi D^2)/(4)`, then:

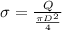`\sigma =(Q)/((\pi D^2)/(4))` (3)

Using (3) on (1):

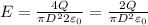`E=(4Q)/(\pi D^2 2\varepsilon_(0))=(2Q)/(\pi D^2 \varepsilon_(0))` (4)

Now if the plastic bead is suspended between the plates by Newton's first law the weight (W) should be compensated by and opposite the electric force (F), so it should be equal in magnitude to the weight:

`W=F`

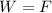
weight is mass times gravity acceleration (mg) and the electric force on an object is:

`F=qE`

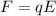
with q the magnitude of charge of the plastic bead and E the magnitude of the electric field between the plates, then:

`qE=mg`

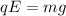
solving for E:

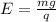`E=(mg)/(q)` (5)

Now we can equate expressions (4) and (5):

`(mg)/(q)=(2Q)/(\pi D^2 \varepsilon_(0))`

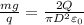
Solving for Q:

`Q=(mg\pi D^2 \varepsilon_(0))/(2q)=((0.0016)(9.81)\pi (0.18)^2 8.85419*10^(-12))/(2*4.4*10^(-9))`

`Q=1.61*10^(-6) C`