Answer:
For any string, we use
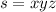
Step-by-step explanation:
The pumping lemma says that for any string s in the language, with length greater than the pumping length p, we can write s = xyz with |xy| ≤ p, such that xyi z is also in the language for every i ≥ 0. For the given language, we can take p = 2.
Here are the cases:
- Consider any string a i b j c k in the language. If i = 1 or i > 2, we take
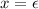 and y = a. If i = 1, we must have j = k and adding any number of a’s still preserves the membership in the language. For i > 2, all strings obtained by pumping y as defined above, have two or more a’s and hence are always in the language.
and y = a. If i = 1, we must have j = k and adding any number of a’s still preserves the membership in the language. For i > 2, all strings obtained by pumping y as defined above, have two or more a’s and hence are always in the language.
- For i = 2, we can take and y = aa. Since the strings obtained by pumping in this case always have an even number of a’s, they are all in the language.
- Finally, for the case i = 0, we take
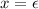 , and y = b if j > 0 and y = c otherwise. Since strings of the form b j c k are always in the language, we satisfy the conditions of the pumping lemma in this case as well.
, and y = b if j > 0 and y = c otherwise. Since strings of the form b j c k are always in the language, we satisfy the conditions of the pumping lemma in this case as well.