Question

Prove the following languages are nonregular, once using the pumping lemma and once using the Myhill-Nerode theorem. When using the pumping lemma, try to use the most general (least restrictive) case:i) The language where the longest string of consecutive a's is longer than the longest string of consecutive b'sii) aibjajiii) aibjck, where k ≤ i+jiv) aibjck, where i is neither the least nor greatest out of i,j, and k.

Answer 1

For any string, we use
`s = xyz`

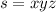
Step-by-step explanation:

The pumping lemma says that for any string s in the language, with length greater than the pumping length p, we can write s = xyz with |xy| ≤ p, such that xyi z is also in the language for every i ≥ 0. For the given language, we can take p = 2.

Here are the cases:

• Consider any string a i b j c k in the language. If i = 1 or i > 2, we take
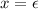  `x = \epsilon` and y = a. If i = 1, we must have j = k and adding any number of a’s still preserves the membership in the language. For i > 2, all strings obtained by pumping y as defined above, have two or more a’s and hence are always in the language.

• For i = 2, we can take and y = aa. Since the strings obtained by pumping in this case always have an even number of a’s, they are all in the language.
• Finally, for the case i = 0, we take
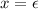  `x = \epsilon` , and y = b if j > 0 and y = c otherwise. Since strings of the form b j c k are always in the language, we satisfy the conditions of the pumping lemma in this case as well.