Question

The "beta coefficient" of a stock is a measure of the stock`s volatility (or risk) relative to the market as a whole. Stocks with beta coefficients greater than 1 generally bear the greater risk (more volatility) than the market, whereas stocks with beta coefficients less than 1 are less risky (less volatile) than the overall market. A random sample of 15 high-technology stocks was selected at the end of 2009, and the sample mean and sample standard deviation of the beta coefficients were computed to be 1.23 and s=.37, respectively. (Assume that the beta coefficient follows a normal distribution.)

a. State the null and alternative hypothesis to test whether the average high-technology stock is riskier than the market as a whole.
b. Establish the appropriate test statistics for this problem.
c. Determine an appropriate decision rule for testing the hypothesis in part a at the level of significance α = .01.
d. Make an appropriate conclusion based on the summary statistics provided in the problem and the decision rule you specified in part c.
e. What is the p-value of the test.
f. Based on the p-value calculated in part (e), do you reject the null hypothesis at the level of significance α=.01? Say how you made your decision.
g. How does your conclusion change if instead of α=.01 we chose a smaller level of significance? Explain.

Answer 1

Explanation:

Hello!

Using the "beta coefficient" as a measure of stock's volatility, a random sample of 15 high-technology stocks was selected at the end of 2009 and their "beta coefficient" was determined, obtaining a sample mean X[bar] = 1.23 and standard deviation S= 0.37

The study variable is:

X: "beta coefficient" of a high-technology stock at the end of 2009.

This variable has a normal distribution: X~N(μ;σ²)

If the beta coefficient is greater than 1, then the volatility of the stock is high.

If the beta coefficient is less than 1, then the stock is less volatile.

a. If the average high-technology stock is riskier than the market as a whole, then we can think that the average "beta coefficient" of the high-technology stocks will be greater than 1, symbolically: μ > 1

Then the statistical hypotheses are:

H₀: μ ≤ 1

H₁: μ > 1

b. Considering that the variable has a normal distribution, there are two possible statistics to use for the test. The standard normal and the student's t.

To use the standard normal you have to know the population variance of the variable. This is unknown, so this statistic won't be of use.

To use the Student's t, there is no need to know the value of the population variance and is more accurate for the estimation or analysis of the population mean when using small samples (less than 30)

So for this test, you have to use the t-test for one sample:

`t= ((X[bar]-Mu))/((S)/(√(n) ) )~t_(n-1)`

`t_(H_0)= (1.23-1)/((0.23)/(√(15) ) ) = 3.87`

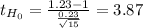
c. This test is one-tailed to the right, this means that you'll reject the null hypothesis at high values of t. To know from which value you can consider it "high value of t" you have to determine the critical value of the test:

`t_(n-1;1-\alpha )= t_(14;0.99)= 2.624`

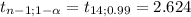
The decision rule is:

If
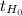`t_(H_0)` ≥ 2.624, then you reject the null hypothesis.

If
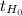`t_(H_0)` < 2.624, then you do not reject the null hypothesis.

d. Considering that
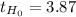`t_(H_0)= 3.87` is greater than the critical value, the decision is to reject the null hypothesis.

Then using a significance level of 1%, there is significant evidence to conclude that the average beta coefficient is greater than 1. The average high-technology stock is riskier than the market as a whole.

e. The p-value is defined as the probability corresponding to the calculated statistic if possible under the null hypothesis (i.e. the probability of obtaining a value as extreme as the value of the statistic under the null hypothesis).

In this case, the p-value is one-tailed as the test and has the same direction (right), under the t-distribution:

P(t₁₄≥3.87)= 1 - P(t₁₄<3.87)= - 1 - 0.9992= 0.0008

p-value= 0.0008

f. The decision rule using the p-value against the significance level is:

If p-value ≤ α, then you reject the null hypothesis.

If the p-value > α, then you do not reject the null hypothesis.

The p-value= 0.0008 is less than α: 0.01, then the decision is to reject the null hypothesis.

g. For the decision to change you'd have to choose a level of significance smaller than the p-value. Using such a small α would lead to an invalid test, then the probability of committing type II error (not rejecting a false null hypothesis) would be too high.

I hope this helps!