Question

Two machines turn out all the products in a factory, with the first machine producing 40%of the product and the second 60%. The first machine produces defective products 2% of the timeand the second machine 4% of the time. Given a defective product, what is the probability it wasproduced on the first machine

Answer 1

Given a defective product, the probability it was produced on the first machine is
`\\ P(F|D) = 0.25`.

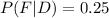Explanation:

This is a case that can be solved using the Bayes' Theorem, which implies conditional probabilities.

We have to remember that in conditional probabilities, the sample space is replaced by the probability of a given event (as can be seen below).

First, we need to find the probability of producing a defective product:

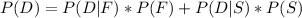`\\ P(D) = P(D|F)*P(F) + P(D|S)*P(S)` (1)

Where

P(D), the probability of producing a defective product.

P(F), the probability that the product was produced by the first machine. In this case, P(F) = 0.40.

P(S), the probability that the product was produced by the second machine. In this case, P(S) = 0.60.

P(D|F), a conditional probability that the product is defective given (or assuming) that it was produced by the first machine. In this case, from the question, P(D|F) = 0.02.

P(D|S), a conditional probability that the product is defective given (or assuming) that it was produced by the second machine. In this case, from the question, P(D|S) = 0.04.

So, from formula (1):

`\\ P(D) = P(D|F)*P(F) + P(D|S)*P(S)`

`\\ P(D) = 0.02*0.40 + 0.04*0.60`

`\\ P(D) = 0.032`

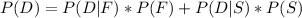
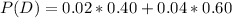
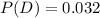
That is, the probability of producing a defective product from these two machines is P(D) = 0.032.

From conditional probabilities we know that:

`\\ P(A \cap B) = P(A|B)*P(B)`

`\\ P(A \cap B) = P(B|A)*P(A) = P(B \cap A)`

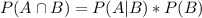
So

`\\ P(A|B)*P(B) = P(B|A)*P(A)`

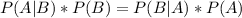
In the same way, we can say that

`\\ P(F|D)*P(D) = P(D|F)*P(F) = P(D \cap F) = P(F \cap D)`

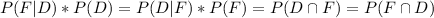
In words, the probability that both events (D and F) occur is given by the "relationship" of conditional probabilities between these two events.

Then

The probability that a product comes from the first machine, given it is defective is as follows:

`\\ P(F|D)*P(D) = P(D|F)*P(F)`

`\\ P(F|D) = (P(D|F)*P(F))/(P(D))`

`\\ P(F|D) = (0.02*0.40)/(0.032)`

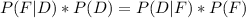
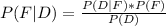
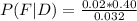
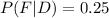`\\ P(F|D) = 0.25` or 25%.

Answer 2

0.4

Explanation:

First Machine(M1) Produces 40% of the product.

P(M1)=40%=0.4

The first Machine Produces defective product(D) 2% of the Time.

P(D)=2%=0.02

Given a defective product(D), we want to find the probability that it was produced on the first machine(M1).

P(M1|D)=P(M1∩D)/P(D)

=(0.4 X 0.02)/0.02

=0.4