Question

A block of mass m = 0.15 kg is set against a spring with a spring constant of k1 = 560 N/m which has been compressed by a distance of 0.1 m. Some distance in front of it, along a frictionless surface, is another spring with a spring constant of k2 = 377 N/m.

a. How far d2, in meters, will the second spring compress when the block runs into it?
b. How fast v, in meters per second, will the block be moving when it strikes the second spring?
c. Now assume friction is present on the surface in between the ends of the springs at their equilibrium lengths, and the coefficient of kinetic friction is? k = 0.5. If the distance between the springs is x = 1 m, how far d2, in meters, will the second spring now compress?

Answer 1

Step-by-step explanation:

a. The compression over the other spring depends of the force that the first spring applies to the block

`F=kx`

`F=kx=(560(N)/(m))(0.1m)=56N`

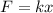
This force allow us to calculate the compression in the other spring

`x'=(F)/(k')=(56N)/(377(N)/(m))=0.14m`

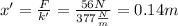
b. We use the expression for the maximum velocity

`v=A\omega`

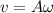
where A is the amplitude 0.1m and w is the angular frecuency, which is calculated

`\omega = \sqrt{(k)/(m)} = \sqrt{(560(N)/(m))/(0.15kg)}=61.10 s^(-1)`

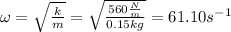
thus

`v=(0.1m)(61.10s^(-1))=6.1(m)/(s)`

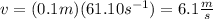
c. Here it is necessary to take into account the change in the kinetic energy due to the work done by the friction force

`E_(k)=(mv^(2))/(2)=2.79J\\f_(k)x=\mu N x= (0.5)(0.15kg*9.8(m)/(s^(2)))(1m)=0.735J\\`

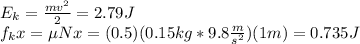
The energy of the block at the moment of starting to compress the other spring is

`E_(k)-f_(k)x=2.05J`

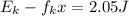
This energy will be potential energy of the other spring, hence

`2.05J=U_(k')=(kx^(2))/(2)`

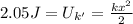
and by taking x' of this las expression we have

`x'=\sqrt{(2(2.05J))/(k')}=\sqrt{(2(2.05J))/(377(N)/(m))}=0.10m`

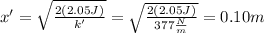
I hope this is useful for you

Regards