Answer:
Equilibrium concentration of
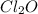 is 0.870 M.
is 0.870 M.
Step-by-step explanation:
Initial concentration of water =
![[H_2O]=1.00 M](https://img.qammunity.org/2021/formulas/chemistry/college/z8ebjnzmpgj6biafuswt54cm2p3sqo9s8m.png)
Initial concentration of
![Cl_2O=[Cl_2O]=1.00 M](https://img.qammunity.org/2021/formulas/chemistry/college/x54hd8bcq8tm5nbyql6l9lfdur6010udz1.png)
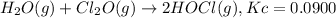
initially
1.00 M 1.00 M 0
At equilibrium
(1.00m-x) M (1.00-x)M 2x
The expression of equilibrium constant is given by :
![K_c=([HOCl]^2)/([H_2O][Cl_2O])](https://img.qammunity.org/2021/formulas/chemistry/college/qd2w9snrmq38xx1fhif4wh7h2zaocnk039.png)
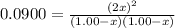
Solving for x :
x = 0.130
Equilibrium concentration of
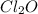 :
:
![[Cl_2O]=(1,00-x) M=1.00 M-0.130 M=0.870 M](https://img.qammunity.org/2021/formulas/chemistry/college/xuoc22mmr9z5k93wdac3ftsgrzanm4v7c1.png)