a)
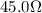
b) 2 A
c) 30 V
d) 2 A
Step-by-step explanation:
a)
Resistors are said to be connected in series when they are connected along the same branch of the circuit: therefore, the current flowing through them is the same (while they can have different potential difference across each of them).
For a series of N resistors, the equivalent resistance is given by the sum of the individual resistances:
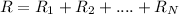
In this problem, we have three resistors, having resistances of:
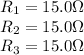
Therefore, the equivalent resistance of the three resistors in series is:
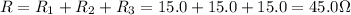
b)
The relationship between voltage frop, current and resistance in a circuit is given by Ohm's Law:
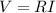
where
V is the potential difference
R is the resistance
I is the current
For this circuit, we have:
V = 90 V is the potential difference across the three resistors in series
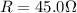 is the equivalent resistance of the circuit
is the equivalent resistance of the circuit
Therefore, the current through the circuit is:
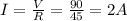
c)
In a series circuit, the current through the resistors is the same, however the voltage frop across each resistor can be different (if they have differnet resistances).
In this case, all the three resistors have same resistance, so the voltage drop across each of them is given again by Ohm's Law:
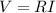
where, in this case
R is the individual resistance
I is the current through the resistor
Here we have:
 is the resistance of each resistor
is the resistance of each resistor
I = 2 A is the current
So, the voltage drop across each resistor is
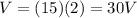
d)
As we said in part b, the current is the same in every part of a circuit in series, since the three resistors are connected in series: so here, the current is 2 A in every point of the circuit.