Question

1. There are three 15.0 Ω resistors connected in series across a 90 V battery.

a) What is the total (equivalent) resistance of the circuit (answer in ohms)? *
b) what is the current in the circuit (answer in amps)? *
c) What is the voltage drop across one of the resistors (answer in Volts)? *
d) What is the current anywhere in the circuit?

Answer 1

a)
`45.0 \Omega`

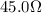
b) 2 A

c) 30 V

d) 2 A

Step-by-step explanation:

a)

Resistors are said to be connected in series when they are connected along the same branch of the circuit: therefore, the current flowing through them is the same (while they can have different potential difference across each of them).

For a series of N resistors, the equivalent resistance is given by the sum of the individual resistances:

`R=R_1+R_2+....+R_N`

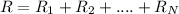
In this problem, we have three resistors, having resistances of:

`R_1=15.0\Omega\\R_2=15.0\Omega\\R_3=15.0\Omega`

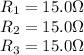
Therefore, the equivalent resistance of the three resistors in series is:

`R=R_1+R_2+R_3=15.0+15.0+15.0=45.0\Omega`

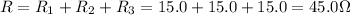
b)

The relationship between voltage frop, current and resistance in a circuit is given by Ohm's Law:

`V=RI`

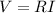
where

V is the potential difference

R is the resistance

I is the current

For this circuit, we have:

V = 90 V is the potential difference across the three resistors in series

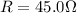`R=45.0 \Omega` is the equivalent resistance of the circuit

Therefore, the current through the circuit is:

`I=(V)/(R)=(90)/(45)=2 A`

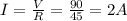
c)

In a series circuit, the current through the resistors is the same, however the voltage frop across each resistor can be different (if they have differnet resistances).

In this case, all the three resistors have same resistance, so the voltage drop across each of them is given again by Ohm's Law:

`V=RI`

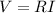
where, in this case

R is the individual resistance

I is the current through the resistor

Here we have:

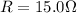`R=15.0\Omega` is the resistance of each resistor

I = 2 A is the current

So, the voltage drop across each resistor is

`V=(15)(2)=30 V`

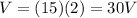
d)

As we said in part b, the current is the same in every part of a circuit in series, since the three resistors are connected in series: so here, the current is 2 A in every point of the circuit.