Question

Trigonometry

Objective: Use trigonometry functions to find the area of triangles.
In ΔEFG, EF=5, EG=8, and m< E=22*. Find the area of ΔEFG, to the nearest tenth of a square unit.

Answer 1

The area of the triangle EFG is 7.4 square units.

Step-by-step explanation:

Given that the measurements of the sides of the triangle are EF = 8, EG = 8 and
`m\angle E=22^(\circ)`

We need to determine the area of the triangle EFG

Area of the triangle:

The area of the triangle EFG can be determined using the formula,

`\text {Area}=(1)/(2) fg \sin E`

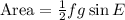
Substituting the values, we get,

`\text {Area}=(1)/(2) (5)(8) \sin 22^(\circ)`

Simplifying the values, we have,

`\text {Area}=(1)/(2)(40)(0.37)`

Multiplying, we get,

`\text {Area}=(14.8)/(2)`

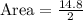
Dividing, we get,

`\text {Area}=7.4`

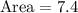
Hence, the area of the triangle EFG is 7.4 square units.