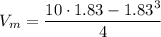Question

We want to construct a box with a square bottom, rectangular sides, and no top. We have exactly 10 ft2 of material for building the box. If we use all of the material in building the box, what is the largest volume we could enclose in the box

Answer 1

`V_m=3.74\ ft^2`

Explanation:

Maximization Using Derivatives

We'll use the first derivative to find the extreme values of a function and then find the value of the independent variables to make the function maximum.

The first step is to produce a model that contains only one variable, take its first derivative and equal it to 0.

Assume a box with a square bottom and rectangular sides. Let's set the sides of the bottom square as x and the height of the box as y. The volume of the box is

`V=x^2y`

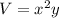
And the total side area is the sum of the bottom square plus the 4 side areas, each one being a rectangle of dimensions x and y. The area is

`A=x^2+4xy`

We know the total material used for the box is
`10 ft^2`

`x^2+4xy=10`

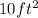
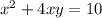
Solving for y

`\displaystyle y=(10-x^2)/(4x)`

The expression for the volume will now be a function only of x:

`\displaystyle V=x^2\cdot (10-x^2)/(4x)`

`\displaystyle V=(10x-x^3)/(4)`

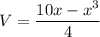
Taking the derivative of V

`\displaystyle V'=(10-3x^2)/(4)`

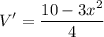
Equating to 0

`\displaystyle (10-3x^2)/(4)=0`

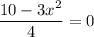
Solving for x

`\displaystyle x=\sqrt{(10)/(3)}=1.83`

`x=1.83\ ft`

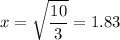
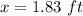
Computing the second derivative:

`\displaystyle V''=(-3x)/(2)`

The second derivative is negative for any positive value of x, thus the extreme value of x is a maximum, and the largest volume of the box is

`\displaystyle V_m=(10\cdot 1.83-1.83^3)/(4)`

`V_m=3.74\ ft^2`