Question

The coordinates of the points bellow represent the vertices of a rectangle: P: (2,2). Q:(6,2) R:(6,5) S:(2,5) What is the perimeter, in units, of rectangle PQRS

Answer 1

Therefore the value of perimeter of the rectangle is 14 in.

Explanation:

The opposite sides of a rectangle are congruent.

The perimeter of a rectangle is 2(length + width)

The area of a rectangle is (length×width).

Given the vertices of a rectangle are P(2,2), Q(6,2), R(6,5) and S(2,5).

To find the the perimeter, first we need the sides of the rectangle.

The distance between two points(x₁,y₁) and (x₂,y₂) is

`=√((x_2-x_1)^2+(y_2-y_1)^2)`

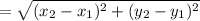
The distance between P and Q is

`=√((6-2)^2+(2-2)^2)` in

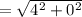`=\sqrt {4^2+0^2}` in

=4 in

The distance between Q and R is

`=\sqrt{(6-6)^2+(5-2)^2` in

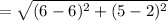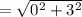`=√(0^2+3^2)` in

=3 in

The distance between R and S is

`=√((2-6)^2+(5-5)^2)` in

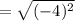`=√( (-4)^2)` in

=4 in

The distance between S and P is

`=√((2-2)^2+(2-5)^2)` in

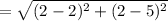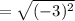`=√((-3)^2)` in

=3 in

Therefore the length of the rectangle is = 4 in.

an the width of the rectangle is = 3 in

Therefore the perimeter of the rectangle is =2(4+3) in

=14 in