Answer:
5.12 mm
Step-by-step explanation:
Let's convert the time taken from hours to seconds
t = 5 h
t =
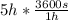
t = 18000 s
The relation expressing the concentration, position and time together is given by the formula:
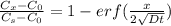
where:
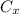 = concentration at depth = 0.206 wt%
= concentration at depth = 0.206 wt%
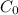 = initial concentration = 0.275 wt%
= initial concentration = 0.275 wt%
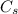 = concentration at the surface position = 0.0 wt%
= concentration at the surface position = 0.0 wt%
D = diffusion coefficient =
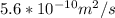
t = time = 18000 s
Replacing the value into the previous formula; we have:
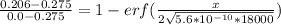
0.2509 = 1 - erf (157.85 x)
erf (157.85 x) = 1 - 0.2509
erf (157.85 x) = 0.7491
So, Let's assume the value of z to be 157.485x ; we have:
z = 157.485 x ------------------ Equation (1)
We obtain the value of Z corresponding to erf (Z) = 0.7491 from the Table 5.1 , 'Table of Error Function Values'
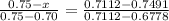
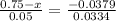
- 0.001895 = (0.75 - z ) 0.0334
- 0.001895 = 0.02505 - 0.0334 z
0.0334 z = 0.02505 + 0.001895
0.0334 z = 0.026945
z =
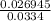
z = 0.806737
Substituting 0.806737 for z in equation (1)
0.806737 = 157.485 x
x =
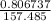
x = 0.00512 m to mm; we have
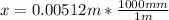
x = 5.12 mm
Thus, the position at which the carbon concentration is 0.206 wt% after a 5 h treatment = 5.12 mm