Question

The production of ethylene glycol from ethylene chlorohydrin and sodium bicarbonate ↑ is carried out in a semibatch reactor. A 1.5-molar solution of ethylene chlorohydrin is fed at a rate of 0.1 mole/minute to 1500 dm3 of a 0.75-molar solution of sodium bicarbonate. The reaction is elementary and carried out isothermally at 30°C where the specific reaction rate is 5.1 dm3/mol/h. Higher temperatures produce unwanted side reactions. The reactor can hold a maximum of 2500 dm3 of liquid. Assume constant density.

Answer 1

See explanation.

Step-by-step explanation:

Hello,

In this case, the undergoing chemical reaction is:

`CH_2OHCH_2Cl+NaHCO_3\rightarrow (CH_2OH)_2+NaCl+CO_2\\A+B\rightarrow C+D+E`

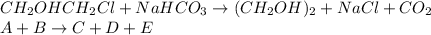
For which the differential equations in terms of the time variation are:

`(dn_A)/(dt)= F_(A,0)+r_AV\\(dn_B)/(dt)=r_BV\\(dn_C)/(dt)=r_CV\\n_D=n_C\\(dV)/(dt)=v_0-(r_CVM_(CO_2))/(\rho )`

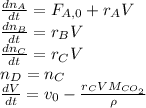
And the implicit equations:

`F_(A,0)=0.1mol/min*60min/1h=6.0mol/h\\v_0=(6.0mol/h)/(1.5mol/dm^3)=4dm^3/h\\rho=1000g/L`

`r_A=-5.1C_AC_B\\r_B=r_A\\r_C=-r_A`

`C_A=(n_A)/(V) \\C_B=(n_B)/(V)`

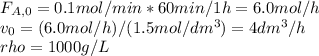
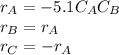
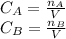
Thus, on the attached pictures you will find the conversion, concentrations, rate and volume profiles as well as the number of moles of ethylene glycol considering a maximum volume of 2500 dm³.

This is the code I used on matlab:

-

t=0;

na(1,1)=0;

nb(1,1)=1125;

nc(1,1)=0;

nd(1,1)=0;

V(1,1)=1500;

k=length(na);

C_A(1,1)=0;

C_B(1,1)=0.75;

x(1,1)=0;

t(1,1)=0;

r_A(k,1)=0;

while V(k,1)<2500

na(k+1,1)=na(k,1)+0.01*(6+r_A(k,1)*V(k,1));

nb(k+1,1)=nb(k,1)+0.01*(r_A(k,1)*V(k,1));

nc(k+1,1)=nc(k,1)+0.01*(-r_A(k,1)*V(k,1));

nd(k+1,1)=nd(k,1)+0.01*(-r_A(k,1)*V(k,1));

V(k+1,1)=V(k,1)+0.01*(4-(-r_A(k,1))*V(k,1)*44/1000);

r_A(k+1,1)=-5.1*C_A(k,1)*C_B(k,1);

C_A(k+1,1)=na(k+1,1)/V(k+1,1);

C_B(k+1,1)=nb(k+1,1)/V(k+1,1);

C_C(k+1,1)=nc(k+1,1)/V(k+1,1);

C_D(k+1,1)=nd(k+1,1)/V(k+1,1);

x(k+1,1)=(nb(1,1)-nb(k+1,1))/nb(1,1);

t(k+1,1)=t(k,1)+0.01;

k=k+1;

end

-

Best regards.

Answer 2

The constant density decreases

Step-by-step explanation:

As the temperature of a solvent increases, the solubility of any gas dissolved in that solvent decreases.

For example:

when the temperature of a river, lake or stream is raised high , due to discharge of hot water from some industrial process the solubility of the oxygen in the water is decreased .The fish and the other organisms that live in the water bodies such as rivers, ponds, lakes etc can survive only in the presence of oxygen and decrease in the concentration of the water due to increased temperature can lead to the death of the fish and this may in turn damage the ecosystem.

In the above example, water is considered as the solvent and the oxygen is considered as the solute. When the temperature of the solvent that is water increases, the solubility of the gas that is oxygen in the solvent decreases.

Therefore the answer is decreases