Question

The opponents of soccer team A are of two types: either they are a class 1 or a class 2 team. The number of goals team A scores against a class i opponent is a Poisson random variable with mean λ , where λ = 2, λ = 3. This weekend the team has two games against teams they are not very familiar with. Assuming that the first team they play is a class 1 team with probability 0.6 and the second is, independently of the class of the first team, a class 1 team with probability 0.3, determine

(a) the expected number of goals team A will score this weekend.
(b) the probability that team A will score a total of five goals.

I need help with part b of this question. I have part a covered. Please explain in detail on how to obtain the answer for part b.

Answer 1

a) The expected number of goals team A will score is 5.1

b) The probability that team A will score a total of 5 goals is 0.1147

Explanation:

Let X be the amount of goals scored by team A in both matches. Let X1 and X2 be the total amount of goals team A scores in match 1 and 2 respectively, then X = X1+X2, and also

a)

E(X) = E(X1+X2) = E(X1)+E(X2) = 0.6*2+0.4*3 + 0.3*2+0.7*3 = 5.1

b) In order for X to be equal to 5 we have 5 possibilities

- X1 is 0 and X2 is 5

- X1 is 1 and X2 is 4

- X1 is 2 and X2 is 3

- X1 is 3 and X2 is 2

- X1 is 4 and X2 is 1

- X1 is 5 and X2 is 0

Let T1 be a poisson distribution with mean λ = 2, then

`P(T1=0) = e^(-2)`

`P(T1=1) = 2 * e^(-2)`

`P(T1=2) = 2 * e^(-2)`

`P(T1=3) = (4)/(3) \, e^(-2)`

`P(T1=4) = (2)/(3)\, e^(-2)`

`P(T1=5) = (4)/(15)\,e^(-2)`

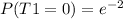
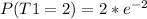
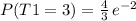
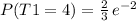
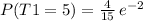
Lets do the same with a Poisson distribution T2 with mean λ = 3

`P(T2=0) = e^(-3)`

`P(T2=1) = 3 \, e^(-3)\\P(T2=2) = (9)/(2) \, e^(-3)\\P(T2=3) = (9)/(2) \, e^(-3)\\P(T2=4) = (27)/(8) \, e^(-3)\\P(T2=5) = (81)/(40) \, e^(-3)`

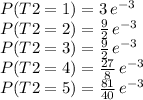
Now, we are ready to compute the probability that X is equal to 5.

`P(X1 = 0, X2 = 5) = (0.6* e^(-2) + 0.4*e^(-3)) * (0.3*(4)/(15)e^(-2) + 0.7*(81)/(40) e^(-3)) = 0.00823\\P(X1 = 1, X2 = 4) = (0.6* 2e^(-2) + 0.4*3 e^(-3)) * (0.3*(2)/(3)e^(-2) + 0.7*(27)/(8) e^(-3)) = 0.03214\\P(X1 = 2, X2 = 3) = (0.6* 2e^(-2) + 0.4*(9)/(2)e^(-3)) * (0.3*(4)/(3)e^(-2) + 0.7*(9)/(2) e^(-3)) = 0.05317\\P(X1 = 3, X2 = 2) = (0.6* (4)/(3)e^(-2) + 0.4*(9)/(2)*e^(-3)) * (0.3*2e^(-2) + 0.7*(9)/(2) e^(-3)) = 0.0471`

`P(X1 = 4, X2 = 1) = (0.6* (2)/(3)e^(-2) + 0.4*(27)/(8)e^(-3)) * (0.3*2e^(-2) + 0.7*3e^(-3)) = 0.0225\\P(X1 = 5, X2 = 0) = (0.6* (4)/(15)e^(-2) + 0.4*(81)/(40)e^(-3)) * (0.3*e^(-2) + 0.7*e^(-3)) = 0.0047`

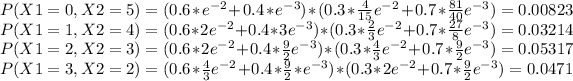
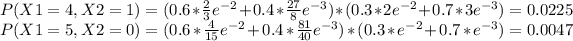
We can conclude that

P(X = 5) = 0.00823+0.03214+0.05317+0.0471+0.0225+0.0047 = 0.1147

The probability that team A will score a total of 5 goals is 0.1147