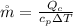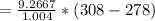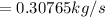Answer:
The rate of fuel required to drive the air conditioner
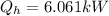
The flow rate of the cold air is

Step-by-step explanation:
From this question we are told that
The efficiency is
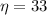 % = 0.33
% = 0.33
Temperature for the hot day is

Temperature after cooling is

The input power is

The rate of fuel required to drive the air conditioner can be mathematically represented as
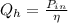
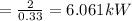
From the question the air condition is assumed to be half as a Carnot refrigeration unit
This can be Mathematically interpreted in terms of COP(coefficient of performance) as
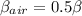
where
 denotes COP and is mathematically represented as
denotes COP and is mathematically represented as
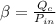
= >
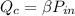
Where
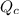 is the rate of flue being burned for cold air to flow
is the rate of flue being burned for cold air to flow
Now if the COP of a Carnot refrigerator is having this value

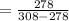
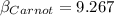
Then

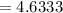
Now substituting the value of
 to solve for
to solve for
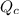
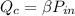
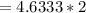
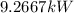
The equation for the rate of fuel being burned for the cold air to flow

Making the flow rate of the cold air