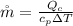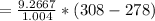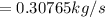Question

A car engine with a thermal efficiency of 33% drives the air-conditioner unit (a refrigerator) besides powering the car and other auxiliary equipment. On a hot (35oC) summer day the A/C takes outside air in and cools it to 5oC sending it into a duct using 2 kW of power input and it is assumed to be half as good as a Carnot refrigeration unit. Find the rate of fuel (kW) being burned extra just to drive the A/C unit and its COP. Find the flow rate of cold air the A/C unit can provide.

Answer 1

The rate of fuel required to drive the air conditioner
`Q_h = 6.061 kW`

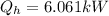
The flow rate of the cold air is
`\r m = 0.30765 kg/s`

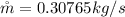
Step-by-step explanation:

From this question we are told that

The efficiency is
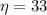`\eta = 33`% = 0.33

Temperature for the hot day is
`T_h = 35^oC = 308 K \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (35+273)`

Temperature after cooling is
`T_c = 5^oC = 278K`

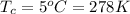
The input power is
`P_(in) = 2kW`

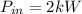
The rate of fuel required to drive the air conditioner can be mathematically represented as

`Q_h = (P_(in))/(\eta)`

`= (2)/(0.33) = 6.061 kW`

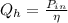
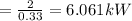
From the question the air condition is assumed to be half as a Carnot refrigeration unit

This can be Mathematically interpreted in terms of COP(coefficient of performance) as

`\beta_(air) = 0.5 \beta`

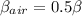
where
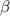`\beta` denotes COP and is mathematically represented as

`\beta = (Q_c)/(P_(in))`

= >
`Q_c = \beta P_(in)`

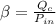
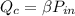
Where
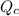`Q_c` is the rate of flue being burned for cold air to flow

Now if the COP of a Carnot refrigerator is having this value

`\beta_(Carnot ) = (T_c)/(T_h - T_c)`

`= (278)/(308-278)`

`\beta_(Carnot) = 9.267\\`

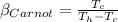
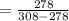
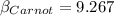
Then

`\beta_(air) = 0.5 * 9.2667`

`= 4.6333`

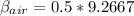
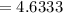
Now substituting the value of
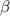`\beta` to solve for
`Q_c`

`Q_c = \beta P_(in)`

`= 4.6333 *2`

`9.2667kW`

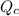
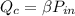
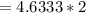
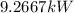
The equation for the rate of fuel being burned for the cold air to flow

`Q_c = \r mc_p \Delta T`

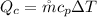
Making the flow rate of the cold air

`\r m = (Q_c)/(c_p \Delta T)`

`= (9.2667)/(1.004)* (308 - 278)`

`= 0.30765 kg/s`