Answer:
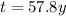
Step-by-step explanation:
The time that will take for nickel to decay can be calculated using the decay equation:

Where:
N(t): is the quantity of Ni that still remains after a time t,
N(0): is the initial quantity of Ni
t: is the time
λ: is the decay constant of Ni
The decay constant can be calculated using the half-life of Ni:
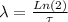
Here:
τ is the half-life (τ = 100 y)
Now, we can write N(t) in terms of N(0), because we know that nickel decay 67% after t time, in other words: N(t)=N(0)*0.67.
Therefore, we can rewrite the decay equation:
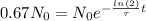
Finally, we just need to find t.
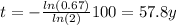
I hope it helps you!