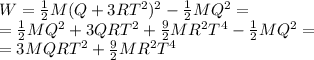Question

A single, nonconstant force acts in the + x ‑direction on an object of mass M that is constrained to move along the x ‑axis. As a result, the object's position as a function of time is x ( t ) = P + Q t + R t 3 How much work W is done by this force from t = 0 s to final time T ? Express the answer in terms of P , Q , R , M , and T .

Answer 1

`3MQRT^2+(9)/(2)MR^2T^4`

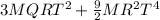
Step-by-step explanation:

In order to find the work done by the force, we use the work-energy theorem, which states that the work done by a force on an object is equal to the change in kinetic energy of the object. Mathematically:

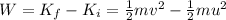`W=K_f-K_i = (1)/(2)mv^2-(1)/(2)mu^2` (1)

where

W is the work done

m is the mass of the object

v is the final speed of the object

u is the initial speed

In this problem, we have:

m = M is the mass of the object

The position of the object at time t is

`x(t)=P+Qt+Rt^3`

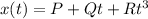
We can find its speed at time t by calculating the derivative of the position:

`v(t)=x'(t)=Q+3Rt^2`

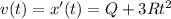
Therefore:

- The speed at time t = 0 is

`u=v(0)=Q`

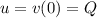
- The speed at time t = T is

`v=v(T)=Q+3RT^2`

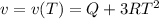
Substituting into eq.(1), we find the work done:

`W=(1)/(2)M(Q+3RT^2)^2-(1)/(2)MQ^2=\\=(1)/(2)MQ^2+3QRT^2+(9)/(2)MR^2T^4-(1)/(2)MQ^2=\\=3MQRT^2+(9)/(2)MR^2T^4`