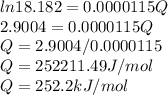Question

An alloy is evaluated for potential creep deformation in a short-term laboratory experiment. The creep rate (ϵ˙) is found to be 1% per hour at 800 ∘C and 5.5×10−2% per hour at 700 ∘C. Calculate the activation energy for creep in this temperature range.

Answer 1

Activation energy for creep in this temperature range is Q = 252.2 kJ/mol

Step-by-step explanation:

To calculate the creep rate at a particular temperature

creep rate,
`\zeta_(\theta) = C \exp((-Q)/(R \theta) )`

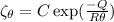
Creep rate at 800⁰C,
`\zeta_(800) = C \exp((-Q)/(R (800+273)) )`

`\zeta_(800) = C \exp((-Q)/(1073R) )\\\zeta_(800) = 1 \% per hour =0.01\\`

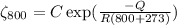
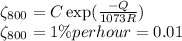
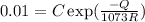`0.01 = C \exp((-Q)/(1073R) )`.........................(1)

Creep rate at 700⁰C

`\zeta_(700) = C \exp((-Q)/(R (700+273)) )`

`\zeta_(800) = C \exp((-Q)/(973R) )\\\zeta_(800) = 5.5 * 10^(-2) \% per hour =5.5 * 10^(-4)`

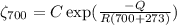
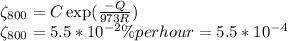
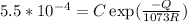`5.5 * 10^(-4) = C \exp((-Q)/(1073R) )`.................(2)

Divide equation (1) by equation (2)

`(0.01)/(5.5 * 10^(-4) ) = \exp[(-Q)/(1073R) -(-Q)/(973R) ]\\18.182= \exp[(-Q)/(1073R) +(Q)/(973R) ]\\R = 8.314\\18.182= \exp[(-Q)/(1073*8.314) +(Q)/(973*8.314) ]\\18.182= \exp[0.0000115 Q]\\`

Take the natural log of both sides

`ln 18.182= 0.0000115Q\\2.9004 = 0.0000115Q\\Q = 2.9004/0.0000115\\Q = 252211.49 J/mol\\Q = 252.2 kJ/mol`