Answer:
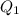 = 7.5
= 7.5
 = 14
= 14
Explanation:
We are given the following data;
6, 7, 8, 9, 11, 13, 14, 14, 18
Now,
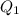 is called the first Quartile of the data which represents the 25% of the data values.
is called the first Quartile of the data which represents the 25% of the data values.
 is called the third Quartile of the data which represents the 75% of the data values.
is called the third Quartile of the data which represents the 75% of the data values.
Now, calculation of quartiles;
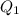 is given by =
is given by =
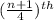 obs. {where n = 9}
obs. {where n = 9}
=
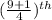 obs
obs
=
 obs =
obs =
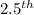 obs
obs
So,
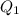 =
=
 obs + 0.5(
obs + 0.5(
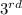 -
-
 )
)
= 7 + 0.5(8-7) = 7 + 0.5 = 7.5
 is given by =
is given by =
 =
=
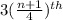 obs. {where n = 9}
obs. {where n = 9}
=
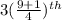 obs
obs
=
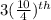 obs =
obs =
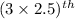 obs =
obs =
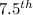 obs.
obs.
So,
 =
=
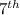 obs + 0.5(
obs + 0.5(
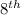 -
-
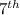 )
)
= 14 + 0.5(14 - 14) = 14 + 0 = 14
Therefore,
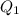 = 7.5 and
= 7.5 and
 = 14.
= 14.