Question

During a tennis serve, a racket is given an angular acceleration of magnitude 170 rad/s2. At the top of the serve, the racket has an angular speed of 18.0 rad/s. If the distance between the top of the racket and the shoulder is 1.10 m, find the magnitude of the total acceleration of the top of the racket.

Answer 1

The magnitude of total acceleration of the top of the racket is 402.5 m/s².

Step-by-step explanation:

Given:

Angular acceleration of racket (α) = 170 rad/s²

Angular speed of the racket (ω) = 18.0 rad/s

Distance between the top of racket and shoulder (r) = 1.10 m

Now, the magnitude of total acceleration is given as the square root of the sum of the squares of its radial and tangential components.

Radial component of acceleration is given as:

`a_r=\omega^2 r=(18)^2* 1.10=324* 1.10=356.4\ m/s^2`

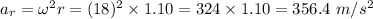
Tangential component of acceleration is given as:

`a_t=r\alpha=1.10* 170=187\ m/s^2`

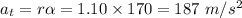
Now, magnitude of total acceleration is given as:

`|a|=√(a_r^2+a_t^2)\\\\|a|=√((356.4)^2+(187)^2)\\\\|a|=402.5\ m/s^2`

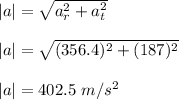
Therefore, the magnitude of total acceleration of the top of the racket is 402.5 m/s².