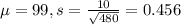Answer:
a) μ = 99 σ = 3.333
b) μ = 99 σ = 2.673
c) μ = 99 σ = 1.69
d) μ = 99 σ = 1.291
e) μ = 99 σ = 0.913
f) μ = 99 σ = 0.456
Explanation:
The Central Limit Theorem estabilishes that, for a random variable X, with mean
 and standard deviation
and standard deviation
 , the sample means with size n of at least 30 can be approximated to a normal distribution with mean
, the sample means with size n of at least 30 can be approximated to a normal distribution with mean
 and standard deviation
and standard deviation
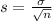
In this problem, we have that:
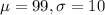
(a) n=9 μ = σ =
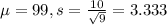
(b) n=14 μ = σ =
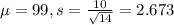
(c) n=35 μ = σ =
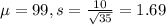
(d) n=60 μ = σ =

(e) n=120 μ = σ =
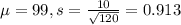
(f) n=480 μ = σ =