Answer:
critical pressure ratio = 108.07 k pa
Step-by-step explanation:
Pt = 200 k Pa
Tt = 800 k
Po = 101.3 k Pa
y = 1.33
R = 287 J/(kg.k)
critical pressure ratio ( Pc )
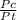 =
=
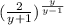 ------- equation 1
------- equation 1
Pt given as 200 k Pa
Y = 1.33
back to equation 1
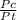 =
=
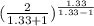
Pc = 200 * 0.5404 = 108.07 k pa