Answer:
The population will become 840 million in 2019.
Explanation:
Given:
The exponential model of population is given as:
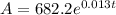
Here, 't' is in years measured since 2003.
This means for the year 2003, t = 0 and so on.
Now, in order to get the year when the population is 840 million, we need to plug in 840 for 'A' and solve for 't'. Therefore,
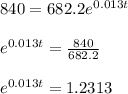
Taking natural log on both sides, we get:

Therefore, 16 years after 2003, the population will be 840 million.
So, the year is equal to 2003 + 16 = 2019.
Hence, in the year 2019, the population will become 840 million.