Answer:
(a)Therefore the maximum height of the object is 16 feet.
(b)Therefore the object hits the ground after 2 seconds.
Explanation:
(a)
Given function of height is
h(t)= 32t-16t²
where t is time in second
[The unit of h(t) is not given, so consider the unit of h(t) in feet]
We know that,
If a function y = ax²+bx+c.
The maximum value of the y is at
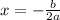
Here a= -16 and b =32.
The object attains its maximum height when
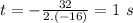
Its means after 1 s , the object attains its maximum height.
Therefore the maximum height of the object is
h(1) = 32.1-16(1)² [putting t= 1]
=32-16
=16 feet
(b)
When the object teaches the ground then height of the object will be zero.
i.e h(t) = 0
Therefore,
32t-16t² =0
⇒16t(2-t)=0
⇒t=0 or, t=2
Therefore the object hits the ground after 2 seconds.