Answer:
a)
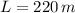 , b)
, b)

Step-by-step explanation:
a) The counterflow heat exchanger is presented in the attachment. Given that cold water is an uncompressible fluid, specific heat does not vary significantly with changes on temperature. Let assume that cold water has the following specific heat:

The effectiveness of the counterflow heat exchanger as a function of the capacity ratio and NTU is:
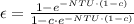
The capacity ratio is:
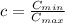

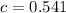
Heat exchangers with NTU greater than 3 have enormous heat transfer surfaces and are not justified economically. Let consider that
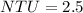 . The efectiveness of the heat exchanger is:
. The efectiveness of the heat exchanger is:

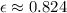
The real heat transfer rate is:
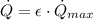
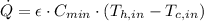
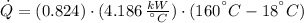
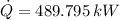
The exit temperature of the hot fluid is:
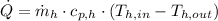
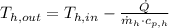
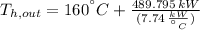
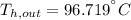
The log mean temperature difference is determined herein:

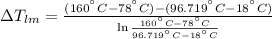
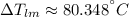
The heat transfer surface area is:
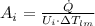

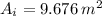
Length of a single pass counter flow heat exchanger is:
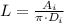

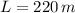
b) Given that tube wall is very thin, inner and outer heat transfer areas are similar and, consequently, the cold side heat transfer coefficient is approximately equal to the hot side heat transfer coefficient.
