Answer:
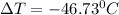

Step-by-step explanation:
Hello,
In this case, since the process is isoenthalpic the given enthalpy remains constant, besides, the temperature at the 132.82 kPa is computed by interpolating the following data:
![\left[\begin{array}{ccc}P(kPa)&T(^0C)\\120&-22.32\\140&-18.77\\132.82&x=-20.044\end{array}\right]](https://img.qammunity.org/2021/formulas/engineering/college/4zsojws1ywj2koi8594kz6a0xvzjrk23sk.png)
Thus, the temperature drop is:

Moreover, the volume is obtained by, at first, computing the thermodynamic data at -20.044 °C by interpolating:
![\left[\begin{array}{ccccc}T(^0C)&hf(kJ/kg)&hfg(kJ/kg)&vf(m^3/kg)&vg(m^3/kg)\\-22.32&22.49&214.48&0.0007324&0.16212\\-18.77&27.08&212.08&0.0007383&0.14014\\-20.044&x=25.43&y=212.94&z=0.0007362&w=0.14802\end{array}\right]](https://img.qammunity.org/2021/formulas/engineering/college/fb27z0rpby2af3nahdpt5wrj42d41lt03s.png)
Then, by knowing the mixture's quality based on the mixture's constant enthalpy:

And finally, the mixtures volume:
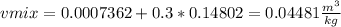
Best regards.