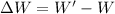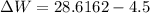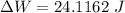Question

If it requires 4.5 J of work to stretch a particular spring by 2.3 cm from its equilibrium length, how much more work will be required to stretch it an additional 3.5 cm

Answer 1

`\Delta W=24.1162\ J`

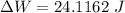
Step-by-step explanation:

Given:

• work done to stretch the spring,
  `W=4.5\ J`

• length through which the spring is stretched beyond equilibrium,
  `\Delta x=2.3\ cm=0.023\ m`

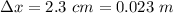
• additional stretch in the spring length,
  `\delta x=3.5\ cm=0.035\ m`

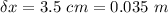
We know the work done in stretching the spring is given as:

`W=(1)/(2) * k.\Delta x^2`

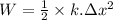
where:

k = stiffness constant

`4.5=0.5* k* 0.023^2`

`k=17013.2325\ N.m^(-1)`

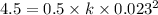
Now the work done in stretching the spring from equilibrium to (
`\Delta x+\delta x`):

`W'=0.5* k.(\Delta x+\delta x)^2`

`W'=0.5* 17013.2325* 0.058^2`

`W'=28.6162\ J`

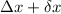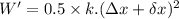
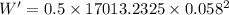
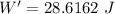
So, the amount of extra work done:

`\Delta W=W'-W`

`\Delta W=28.6162-4.5`

`\Delta W=24.1162\ J`